堆疊的抽象資料結構
堆疊 (stack) 是一種受限制的線性 (linear) 資料結構,僅能由單一出入口存取資料。堆疊的存取方式為 FILO (First-In, Last-Out),讀者可以將堆疊想像成一個長桶子,先放入的東西位於桶子的下方,後放入的東西位於桶子的上方。

堆疊的抽象資料結構如下:
S is a stack.
sub IsEmpty(S): bool
(Optional) sub IsFull(S): bool
(Optional) sub Size(S): size >= 0
sub Peek(S): data
sub Push(S, data): void
sub Pop(S): data由此可知,堆疊至少有以下四個公開行為:
IsEmpty(S):檢查堆疊是否為空Peek(S):檢視堆疊最上方的元素,堆疊大小不變Push(S, data):存入新的元素,堆疊大小加 1Pop(S):取出堆疊最上方的元素,堆疊大小減少 1
以下兩個是選擇性的:
IsFull(S):檢查堆疊是否已滿Size(S):回傳堆疊的大小
堆疊型態的公開界面
以下是堆疊型態的公開界面:
#ifndef STACK_H
#define STACK_H
#ifndef __cplusplus
#include <stdbool.h>
#endif
typedef struct stack_t stack_t;
#ifdef __cplusplus
extern "C" {
#endif
stack_t * stack_new(void);
void stack_delete(void *self);
bool stack_is_empty(const stack_t *self);
int stack_peek(const stack_t *self);
bool stack_push(stack_t *self, const int data);
int stack_pop(stack_t *self);
#ifdef __cplusplus
}
#endif
#endif /* STACK_H */扣除建構函式和解構函式外,這個堆疊型態有四個公開操作,算是中規中矩的界面。
我們使用 forward declaration 來製作 opaque pointer,這是為了防止外部程式直接接觸堆疊型態的屬性。在這樣的宣告下,只能使用我們宣告的函式來操作堆疊。我們在之後的資料結構也會採用這種方式。
宣告堆疊型態
以串列實作堆疊時,通常會用額外的 node_t 類別做為內部儲存資料的節點:
typedef struct node node_t;
struct node {
int data;
node_t *next;
};有節點型態後,就可以宣告堆疊型態:
typedef struct stack stack_t;
struct stack {
node_t *top;
};如果想要取得堆疊的大小,建議額外新增一個屬性,用來儲存堆疊的大小。每次推入 (或移出) 元素時就將堆疊大小加 (或減) 一。
堆疊使用雙向連結節點沒有額外的好處,故此處使用單向節點。
有些資料結構的教材會採用類似以下的宣告:
typedef struct node node_t; /* 1 */
typedef node_t * node_p; /* 2 */
struct node { /* 3 */
int data; /* 4 */
node_p next; /* 5 */
}; /* 6 */
typedef struct stack stack_t; /* 7 */
struct stack { /* 8 */
node_p top; /* 9 */
}; /* 10 */本範例的關鍵處是我們在第 2 行時用 node_p 做為指標型別 node_t * 的別名。之後分別在第 5 行及第 9 行使用該別名。
一般來說,不建議對指標型別用別名,因為我們會在心理上誤以為該變數不是指標,因而造成撰碼時的錯誤。如果要對指標型別做別名,要在名稱上加上一些可辨識的名稱,像是 _p 或 Ptr 等做為別名的後綴。我們之後不會採用這種方式撰寫程式碼。
堆疊的建構函式
以 C 語言實作堆疊的的建構函式:
stack_t * stack_new()
{
stack_t *s = malloc(sizeof(stack_t));
if (!s)
return s;
s->top = NULL;
return s;
}malloc() 呼叫實際上是有可能失敗的,故需撰寫錯誤處理相關的程式碼。這裡在 malloc() 呼叫失敗時,回傳空的指標。
堆疊的解構函式
堆疊內部的節點以連結串列的方式相接,我們要逐一釋放掉這些節點。我們會用到兩個額外的指標,curr 和 temp,curr 一開始指向內部節點的頭端,而 temp 是暫存值。
一開始先將 temp 指向 curr 所在的節點:
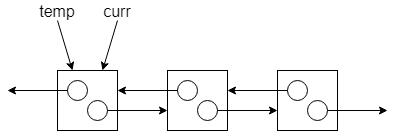
我們將 curr 移至下一個節點,這時候就可以將 temp 所在的節點釋放掉:
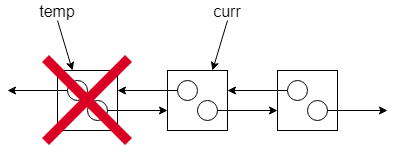
重覆這個動作,就可以把所有的內部節點釋放掉。實際上這些動作會寫在迴圈裡,就可以自動迭代。
以下是解構函式的 C 語言實作:
void stack_delete(void *self)
{
if (!self)
return;
node_t *curr = ((stack_t *) self)->top;
while (curr) {
node_t *temp = curr;
curr = curr->next;
free(temp);
}
free(self);
}釋放記憶體時要由內而外釋放,要不然會無法追蹤內部節點的記憶體區塊。
檢查堆疊是否為空
堆疊的頂端本身是一個指標,檢查該指標是否為空,即可確認堆疊是否為空。以下是 C 語言實作:
bool stack_is_empty(const stack_t *self)
{
assert(self);
return !(self->top) ? true : false;
}此處的 top 是指標,我們以 top 是否為空來檢查堆疊是否為空。
除了這個方式,可以在類別中多放一個欄位,用來存堆疊大小的資訊,這樣就不用每次都從頭開始算,也可以用來檢查堆疊大小是否為 0。
檢視堆疊頂端的資料但不取出
以下是檢視堆疊頂端資料的 C 程式碼:
int stack_peek(const stack_t *self)
{
assert(!stack_is_empty(self));
return self->top->data;
}要先確認堆疊不為空,之後直接存取首節點的資料即可。
將資料推入堆疊
先建立一個新的資料節點 (node),將該節點指向 top 所在的節點,並將 top 也指向該節點:
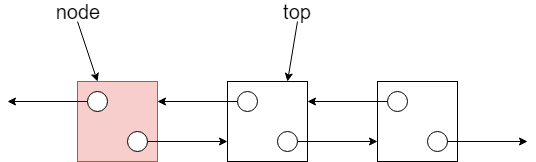
接著再將 top 重新指向該節點即可:
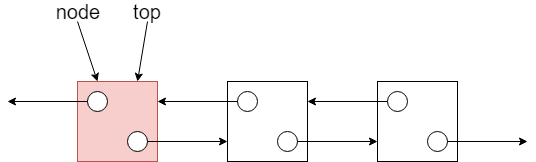
以下是將資料推入堆疊的 C 程式碼:
bool stack_push(stack_t *self, int data)
{
node_t *n = node_new(data);
if (!n) {
return false;
}
n->next = self->top;
self->top = n;
return true;
}由於這裡牽涉到配置記憶體,故我們的公開界面會回傳布林值,表示程式成功與否的狀態。
不論目前首節點為 NULL 或有節點存在,本虛擬碼皆適用,讀者可試著追蹤一下程式碼即可了解。
以下是 node_new 的參考實作:
static node_t * node_new(const int data)
{
node_t *n = malloc(sizeof(node_t));
if (!n) {
return n;
}
n->data = data;
n->next = NULL;
return n;
}將資料從堆疊取出
為了要將資料移出堆疊,我們會用到一個額外的指標 curr。一開始先將 curr 指向 top 所在的節點:
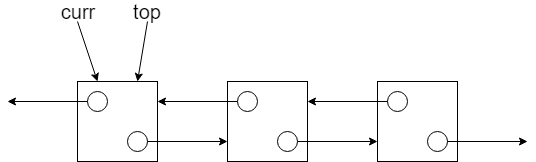
將 top 移往下一個節點後,就可以將 curr 指向的節點釋放掉:
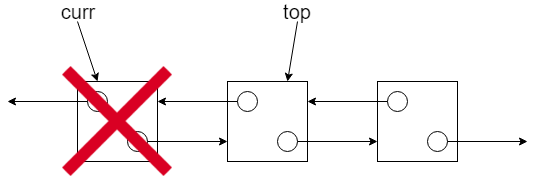
如果堆疊只有單一節點呢?這時候同樣的步驟也成立,只是 top 在移動後會剛好指向空值 (NULL)。
以下是將資料從堆疊取出 C 語言實作:
int stack_pop(stack_t *self)
{
assert(!stack_is_empty(self));
node_t *temp = self->top;
int popped = temp->data;
self->top = temp->next;
free(temp);
return popped;
}由於我們一開始就先排除堆疊為空的情形,之後的虛擬碼是建立在堆疊不為空的假設上。只要將頭端指標指向下一個節點後釋放原節點即可。即使下一個節點為 NULL,本虛擬碼仍適用,讀者可自行追蹤虛擬碼即可了解。
在演算法上的效率
根據本範例的實作得到的程式效率如下:
IsEmpty:O(1)Peek:O(1)Push:O(1)Pop:O(1)
由於 malloc 和 free 是函式,實際上的效率會因實作而異。如果考試或檢定將 malloc 和 free 函式的效率視為 O(1),那麼 Push 和 Pop 的效率就會是 O(1)。我們在後續的文章中,不特別考慮 malloc 和 free 的效率。









